Build makemore
2025年4月2日
18:49
MLP: Activations & Gradients, BatchNorm
关于初始化神经网络的参数,网络训练之前应该考虑的问题:
what loss do you expect at initialization? like uniform distribution of 27 characters
You don't want the output of tanh function to be land on -1 or 1 region, because the gradient of tanh in this region is zero , therefore can't pass gradient backwards.
tanh ,sigmoid, relu都有这个问题,即都存在导数等于0的平坦区域。
如果一个神经元dead,说明无论input如何变化 ,该神经元的激活值,即tanh(h)总是落在导数为0的区域,使得梯度无法传播。相当于never activates.
神经元永久失活可能发生在Initialization时,也可能发生在训练过程中,比如在某个batch上更新参数后,下一个batch中所有样本在该神经元上的激活值都落在了导数为0的区域,反向传播也就不会对参数进行更新,也就相当于这个batch没有对参数进行更新,下下一个batch进来,可能还是不会更新...一直重复下去。
关于Initialization的另一点,x和w都是标准正态分布,x@w的均值是0,但是方差不是1,要想使(x@w)的分布也是均值为0,方差为1(落在激活区域),那么在初始化w的时候就不应该用标准正态分布初始化,详见pytorch中的kaiming_normal及paper。
Batchnorm的出发点,你想让隐藏层神经层的激活值分布在均值=0,方差为1,为什么不直接对激活值做standardization呢。因此Batchnorm层在激活函数之前 。
我们只是想在initialization的时候,不想让神经元失活,而不是一直让神经元的预激活值在训练过程中保持标准正态分布,我们想让back propogate告诉我们预激活值应该如何分布,所以batchnorm有两个可学习参数。
Batchnorm的inefficiency。Batch中的每个样本不是独立的了,当前样本的forward pass需要计算与batch中其他样本的均值,也就将batch中各个样本的前向传播耦合在了一起,而非独立进行。另一方面,当batch中其他样本换成别的样本,forward pass 也会发生变化 ,也就是与batch如何划分有关,使得模型训练变得不desireable。
# Let's train a deeper network
# The classes we create here are the same API
as nn.Module in PyTorch
class Linear:
def __init__(self, fan_in,
fan_out, bias=True):
self.weight = torch.randn((fan_in, fan_out),
generator=g)
/
fan_in**0.5 W的初始化,假设x是normal gaussion分布,w也是normal gaussion,那么w*x的均值仍是0,但标准差不是1,会被放大,也就是说w*x不是norm gaussion。所以w 除以fan_in**0.5的目的是 防止wx的分布不是均值为0,方差为1的分布。关于为什么除以fan_in**0.5,而与fan_out的维度无关,我的想法是因为x是个n*fan_in矩阵,w是个fan_in*fan_out矩阵,w*x中的每个元素是两个向量的点积,向量的长度是fan_in,所以w*x的缩放取决于fan_in,而与fan_out无关。pytorch里是均匀分布。但是当网络很深时,it becomes harder and harder to precisely set the weights and bias in
such way that activations are roughly uniform, 从而引出了batchnorm。
self.bias
= torch.zeros(fan_out)
if bias else
None
def
__call__(self, x):
self.out
= x @
self.weight
if
self.bias is
not None:
self.out
+= self.bias
return
self.out
def
parameters(self):
return
[self.weight] + ([] if self.bias is None
else [self.bias])
class BatchNorm1d:
def __init__(self, dim, eps=1e-5, momentum=0.1): ★ pytorch默认是momentum是0.1,公式是(1-momentum)*v +
momentum*v' 。
momentum的设置需要考虑batchsize,如果batchsize 很大,那么每个batch的均值和方差基本没啥变化,momentum可以设置的大一些,如0.1,表示用最近10个batch的平均,如果batchsize很小,那么momentum应该设置的小一些。
self.eps =
eps
self.momentum = momentum
self.training = True
# parameters (trained with backprop)
self.gamma = torch.ones(dim)
self.beta = torch.zeros(dim)
# buffers (trained with a running 'momentum
update')
self.running_mean = torch.zeros(dim)
self.running_var = torch.ones(dim)
def __call__(self, x):
# calculate the forward pass
if self.training:
xmean = x.mean(0, keepdim=True)
# batch
mean
xvar = x.var(0, keepdim=True) # batch variance
else:
xmean = self.running_mean
xvar = self.running_var
xhat = (x - xmean) / torch.sqrt(xvar + self.eps) # normalize to unit variance
self.out = self.gamma * xhat + self.beta
# update the buffers
if self.training:
with torch.no_grad():
self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * xmean
self.running_var = (1 - self.momentum) * self.running_var + self.momentum * xvar
return self.out
def parameters(self):
return [self.gamma, self.beta]
class Tanh:
def
__call__(self, x):
self.out
= torch.tanh(x)
return
self.out
def
parameters(self):
return
[]
n_embd
= 10 #
the dimensionality of the character embedding vectors
n_hidden = 100 # the number of neurons in the hidden layer of the MLP
g = torch.Generator().manual_seed(2147483647) # for reproducibility
C = torch.randn((vocab_size, n_embd), generator=g)
layers =
[
Linear(n_embd * block_size, n_hidden,
bias=False), BatchNorm1d(n_hidden), Tanh(), ★ 加了batchnorm层之后 ,之前的全连接层就不需要加偏置b了。即bias=False
Linear( n_hidden, n_hidden, bias=False), BatchNorm1d(n_hidden),
Tanh(),
Linear( n_hidden, n_hidden, bias=False), BatchNorm1d(n_hidden),
Tanh(),
Linear( n_hidden, n_hidden, bias=False), BatchNorm1d(n_hidden),
Tanh(),
Linear( n_hidden, n_hidden, bias=False), BatchNorm1d(n_hidden),
Tanh(),
Linear( n_hidden, vocab_size, bias=False), BatchNorm1d(vocab_size),
]
# layers = [
#
Linear(n_embd * block_size, n_hidden), Tanh(),
#
Linear( n_hidden,
n_hidden), Tanh(),
#
Linear( n_hidden,
n_hidden), Tanh(),
#
Linear( n_hidden,
n_hidden), Tanh(),
#
Linear( n_hidden,
n_hidden), Tanh(),
#
Linear( n_hidden,
vocab_size),
# ]
with torch.no_grad():
# last layer: make less
confident
layers[-1].gamma *= 0.1
#layers[-1].weight *= 0.1
# all other layers: apply gain
for layer in layers[:-1]:
if isinstance(layer, Linear):
layer.weight *= 1.0 #5/3 ★当不加batchnorm时,需要乘以5/3相当于把w放大了一些,原因是tanh将输出缩小到-1,1,所以需要放大来抵消tanh的缩小作用。加了batchnorm后,就不需要*5/3了,乘以1保持原状即可。5/3被称为tanh的gain,linear和conv,sigmoid的gain都是1, relu的gain是根号2。
parameters
= [C] +
[p for layer in layers for p in layer.parameters()]
print(sum(p.nelement() for p in
parameters)) # number of parameters in total
for p in
parameters:
p.requires_grad
= True
# same optimization as last time
max_steps = 200000
batch_size = 32
lossi = []
ud = []
for i in
range(max_steps):
# minibatch construct
ix = torch.randint(0, Xtr.shape[0], (batch_size,),
generator=g)
Xb, Yb = Xtr[ix], Ytr[ix] # batch
X,Y Xb的shape:
(batch_size, context length)
# forward pass
emb = C[Xb] # embed
the characters into vectors emb的shape:
(batch_size, context length,embedding_length)
x = emb.view(emb.shape[0], -1) #
concatenate the vectors x的shape: (batch_size,context_length
* embedding_length),也就相当于把context_length个字母的embedding concat起来。也就是将context中所有token(这里是单个字母)的embedding concat起来,平等地对待,而没有按照每个token的embedding区分对待。wavenet缓解了这个问题,wavenet逐级分层地将context中所有token的Embedding fuse起来,而不是一下子concat。wavenet每次concat 2个相邻的token的embedding,经过 context_length/2次操作,实现了将所有token concat起来的目标。
for layer in layers:
x = layer(x)
loss = F.cross_entropy(x, Yb) # loss
function
# backward pass
for layer in layers:
layer.out.retain_grad() #
AFTER_DEBUG: would take out retain_graph 默认情况下,非叶节点的梯度值在反向传播过程中使用完后就会被清除,不会被保留。只有叶节点的梯度值能够被保留下来。 叶子节点是由用户创建的,如w和b,非叶子节点即中间节点如这里的out,在loss.backwad执行后,默认不会保存非叶子节点的grad。
for p in parameters:
p.grad = None
loss.backward()
# update
lr = 0.1 if i < 150000 else 0.01 # step
learning rate decay
for p in parameters:
p.data += -lr * p.grad
# track stats
if
i % 10000 ==
0: # print every once in a while
print(f'{i:7d}/{max_steps:7d}: {loss.item():.4f}')
lossi.append(loss.log10().item())
with
torch.no_grad():
ud.append([((lr*p.grad).std() /
p.data.std()).log10().item()
for p in
parameters])
if i >=
1000:
break # AFTER_DEBUG: would take out obviously to run full
optimization
可视化各层的激活值,forward方向
# visualize histograms
plt.figure(figsize=(20, 4)) # width and height of
the plot
legends = []
for i, layer in enumerate(layers[:-1]): # note: exclude the output layer
if
isinstance(layer, Tanh):
t =
layer.out
print('layer %d (%10s): mean %+.2f,
std %.2f, saturated: %.2f%%' % (i, layer.__class__.__name__,
t.mean(), t.std(),
(t.abs() >
0.97).float().mean()*100))
hy, hx =
torch.histogram(t, density=True)
plt.plot(hx[:-1].detach(),
hy.detach())
legends.append(f'layer
{i} ({layer.__class__.__name__}')
plt.legend(legends);
plt.title('activation distribution')
我们希望各层的激活值,也就是tanh的输出不要落在接近-1或1的区域,因为该区域梯度为0,
我们不希望如下的结果,各层的饱和率太高,各层的激活值大部分落在接近-1和1的区域
layer 1 ( Tanh): mean -0.04, std 0.80, saturated: 30.34%
layer 3 ( Tanh): mean -0.01, std 0.77, saturated: 20.75%
layer 5 ( Tanh): mean -0.01, std 0.78, saturated: 22.75%
layer 7 ( Tanh): mean -0.05, std 0.78, saturated: 21.50%
layer 9 ( Tanh): mean -0.00, std 0.77, saturated: 20.38%
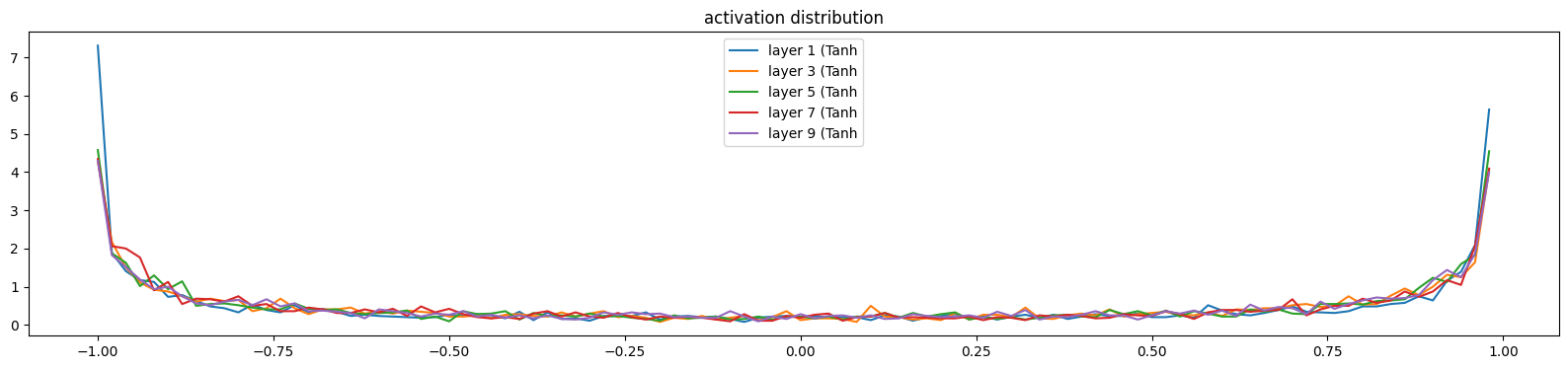
我们希望如下图的结果,
layer 1 ( Tanh): mean -0.04, std 0.64, saturated: 5.19%
layer 3 ( Tanh): mean -0.01, std 0.54, saturated: 0.41%
layer 5 ( Tanh): mean +0.01, std 0.53, saturated: 0.47%
layer 7 ( Tanh): mean -0.02, std 0.53, saturated: 0.28%
layer 9 ( Tanh): mean +0.01, std 0.54, saturated: 0.25%
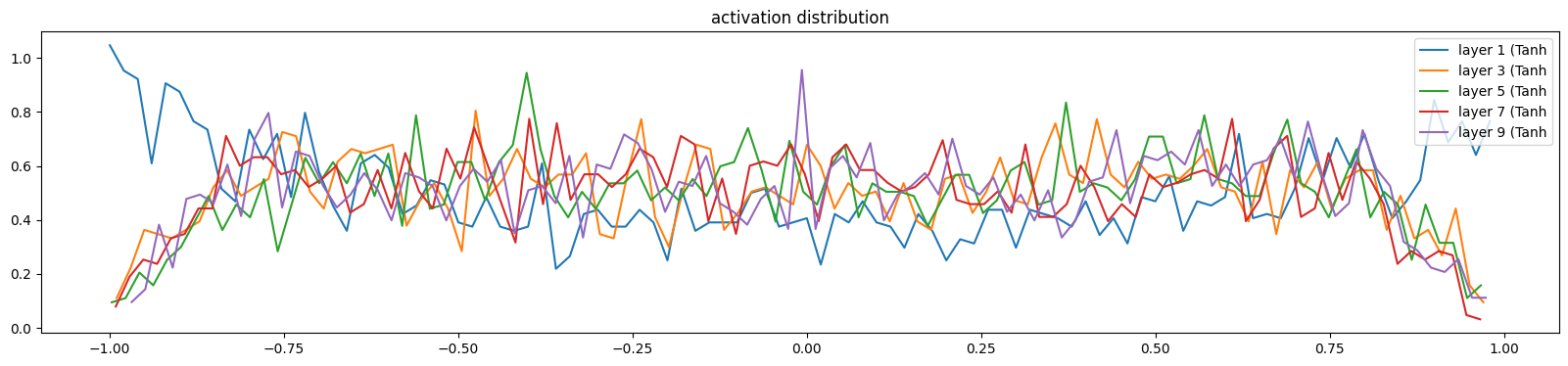
可视化各输出的梯度值,backward方向
# visualize histograms
plt.figure(figsize=(20, 4)) # width and height of
the plot
legends = []
for i, layer in enumerate(layers[:-1]): # note: exclude the output layer
if
isinstance(layer, Tanh):
t =
layer.out.grad
print('layer %d (%10s): mean %+f, std
%e' % (i, layer.__class__.__name__, t.mean(), t.std()))
hy, hx =
torch.histogram(t, density=True)
plt.plot(hx[:-1].detach(),
hy.detach())
legends.append(f'layer
{i} ({layer.__class__.__name__}')
plt.legend(legends);
plt.title('gradient distribution')
我们希望各层out的梯度值,是均匀的,而不是有些层梯度过大,有些层梯度过小,
我们不希望如下 的结果:前面几层梯度大,越往后面层梯度过小
layer 1 ( Tanh): mean -0.000086, std 1.620851e-02
layer 3 ( Tanh): mean +0.000071, std 1.012546e-02
layer 5 ( Tanh): mean +0.000057, std 5.541695e-03
layer 7 ( Tanh): mean +0.000013, std 3.469306e-03
layer 9 ( Tanh): mean +0.000030, std 2.318119e-03
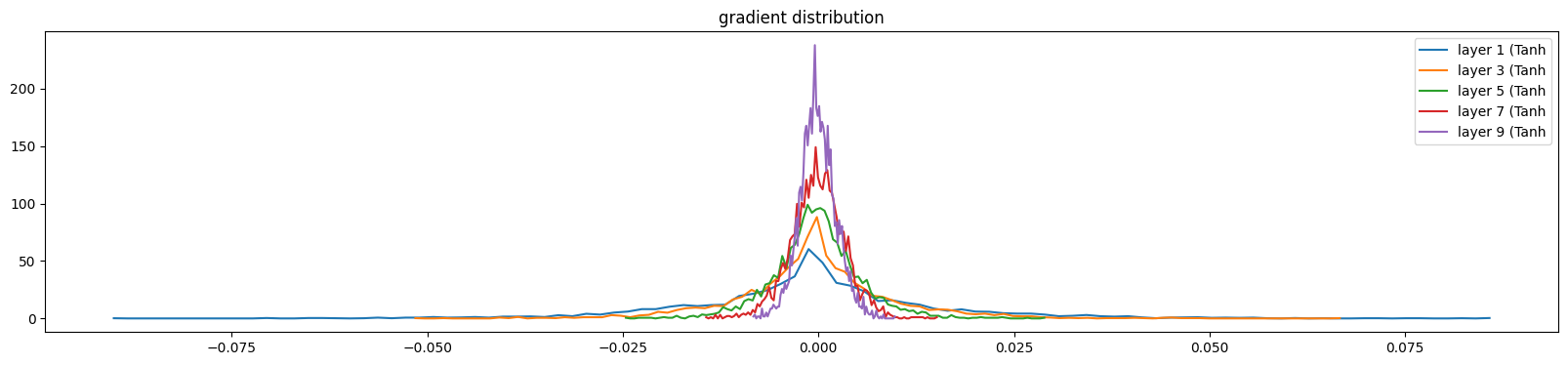
我们希望如下的结果:
layer 1 ( Tanh): mean +0.000033, std 2.641852e-03
layer 3 ( Tanh): mean +0.000043, std 2.440831e-03
layer 5 ( Tanh): mean -0.000004, std 2.338152e-03
layer 7 ( Tanh): mean +0.000006, std 2.283551e-03
layer 9 ( Tanh): mean +0.000040, std 2.059027e-03
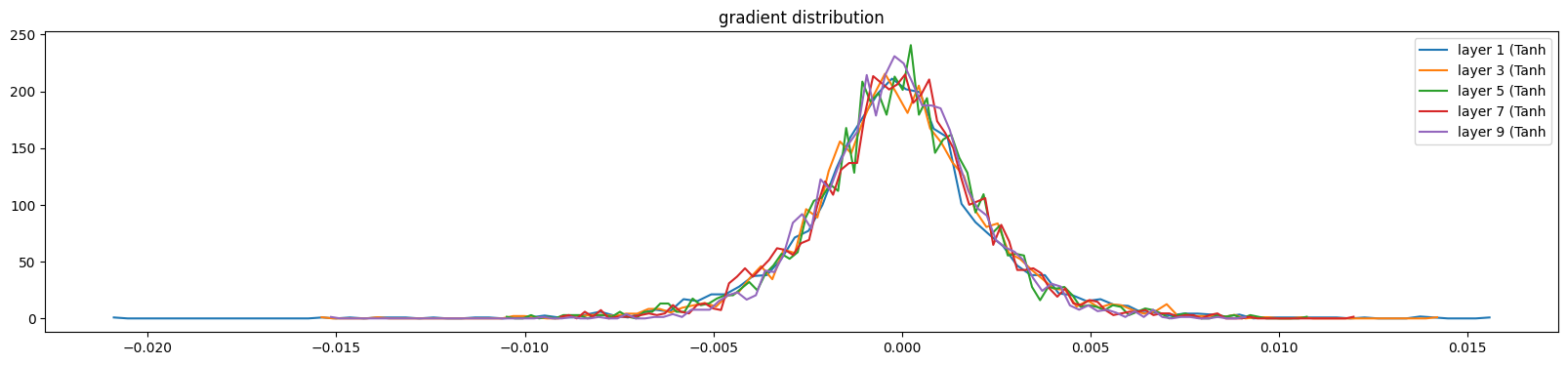
参数w的scale及w的梯度的scale
# visualize histograms
plt.figure(figsize=(20, 4)) # width and height of the plot
legends = []
for i,p in enumerate(parameters):
t = p.grad
if p.ndim == 2:
print('weight %10s | mean %+f | std %e | grad:data ratio %e' % (tuple(p.shape), t.mean(), t.std(), t.std() / p.std()))
hy, hx = torch.histogram(t, density=True)
plt.plot(hx[:-1].detach(), hy.detach())
legends.append(f'{i} {tuple(p.shape)}')
plt.legend(legends)
plt.title('weights gradient distribution');
layer 1 ( Tanh): mean +0.000033, std 2.641852e-03
layer 3 ( Tanh): mean +0.000043, std 2.440831e-03
layer 5 ( Tanh): mean -0.000004, std 2.338152e-03
layer 7 ( Tanh): mean +0.000006, std 2.283551e-03
layer 9 ( Tanh): mean +0.000040, std 2.059027e-03
我们希望w.grad.std()/w.std()的ratio在1e-3左右。也就是不希望w.grad相比于w变化太快。
总结:加了batchnorm后,模型训练 变得robust,不需要考虑如何初始化参数,以及gain,w=w*fan_in**0.05这些。
Building makemore Part 5: Building a WaveNet
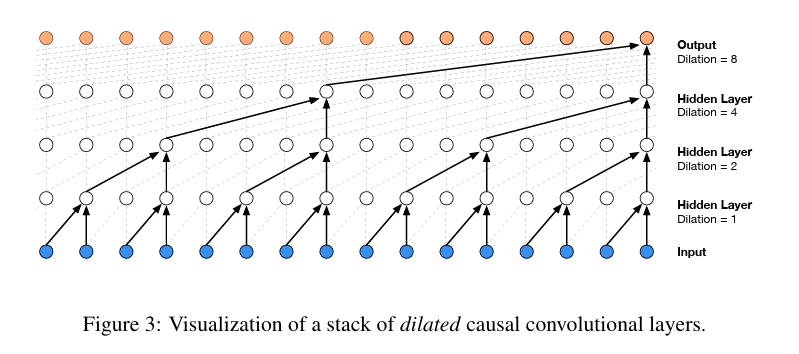
★上图中红框表示 linear层,8个linear层的参数是共享的。
#
-----------------------------------------------------------------------------------------------
Linear层的定义不需要改变,linear层的核心是self.out = x @
self.weight,本质是pytorch矩阵乘法,而矩阵乘法不需要两个矩阵都是2维的,只需要保证第一个矩阵的最后一维的维数和第二个矩阵第一个维度的维数相等即可。利用这个性质,当需要将输入x两两一组进行分组,然后将分组后的数据输入到Linear层时,可以只创建一个linear层,即参数共享+并行,而不是创建context_length/2个linear层,(当然也可以实现创建context_length/2个linear层)。
class Linear:
def __init__(self, fan_in, fan_out, bias=True):
self.weight = torch.randn((fan_in, fan_out)) / fan_in**0.5 # note: kaiming init
self.bias = torch.zeros(fan_out) if bias else None
def __call__(self, x):
self.out = x @ self.weight
if self.bias is not None:
self.out += self.bias
return self.out
def parameters(self):
return [self.weight] + ([] if self.bias is None else [self.bias])
#
-----------------------------------------------------------------------------------------------
class BatchNorm1d:
def
__init__(self, dim, eps=1e-5, momentum=0.1):
self.eps
= eps
self.momentum
= momentum
self.training
= True
# parameters (trained with backprop)
self.gamma
= torch.ones(dim)
self.beta
= torch.zeros(dim)
# buffers (trained with a running 'momentum update')
self.running_mean
= torch.zeros(dim)
self.running_var
= torch.ones(dim)
def
__call__(self, x):
# calculate the forward pass
if self.training:
if
x.ndim == 2:
dim = 0
elif x.ndim == 3: ★注意这里batchnorm的实现和我理解总结的pytorch的batchnorm用法一致,nlp中feature个数是n_embedding的个数,统计均值时,计算的时当前batch中所有句子的所有token的某一维embedding的均值。
dim = (0,1)
xmean = x.mean(dim, keepdim=True) # batch mean
xvar =
x.var(dim, keepdim=True) # batch variance
else:
xmean = self.running_mean
xvar =
self.running_var
xhat = (x - xmean) / torch.sqrt(xvar + self.eps) # normalize to unit variance
self.out
= self.gamma * xhat + self.beta
# update the buffers
if self.training:
with torch.no_grad():
self.running_mean = (1 - self.momentum) * self.running_mean
+ self.momentum
* xmean
self.running_var = (1 - self.momentum) * self.running_var
+ self.momentum
* xvar
return
self.out
def
parameters(self):
return [self.gamma, self.beta]
#
-----------------------------------------------------------------------------------------------
class Tanh:
def __call__(self, x):
self.out =
torch.tanh(x)
return self.out
def parameters(self):
return []
# -----------------------------------------------------------------------------------------------
定义Embedding层,原来Embedding层就是个权重表。
class Embedding:
def __init__(self, num_embeddings, embedding_dim):
self.weight = torch.randn((num_embeddings, embedding_dim))
def __call__(self, IX):
self.out = self.weight[IX]
return self.out
def parameters(self):
return [self.weight]
# -----------------------------------------------------------------------------------------------
FlattenConsecutive的作用:输入x的shape是 B,T,C,B是batchsize,T是context_length,C是n_embedding,在build makemore mlp部分中,是将context_length个字母的embedding直接concat起来,即输出的shape是 B,T*C。而wavenet现在需要将context_length个字母进行相邻字母两两组合,输出的shape是 B,T//2,C*2
class FlattenConsecutive:
def __init__(self, n):
self.n = n
def __call__(self, x):
B, T, C = x.shape
x = x.view(B, T//self.n, C*self.n)
if x.shape[1] == 1:
x = x.squeeze(1)
self.out = x
return self.out
def parameters(self):
return
[]
#
-----------------------------------------------------------------------------------------------
class Sequential:
def __init__(self, layers):
self.layers =
layers
def __call__(self, x):
for layer in
self.layers:
x = layer(x)
self.out =
x
return self.out
def parameters(self):
# get parameters of all layers and stretch them out into one
list
return [p for layer in self.layers for p in layer.parameters()]
开始构建模型
torch.manual_seed(42); # seed rng for reproducibility
# original network
# n_embd = 10 # the
dimensionality of the character embedding vectors
# n_hidden = 300 # the
number of neurons in the hidden layer of the MLP
# model = Sequential([
# Embedding(vocab_size, n_embd),
# FlattenConsecutive(8), Linear(n_embd * 8,
n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
# Linear(n_hidden, vocab_size),
# ])
# hierarchical network
block_size = 8 # context length: how many characters do we take to predict the next one?
n_embd = 24 #
the dimensionality of the character embedding vectors
n_hidden = 128 #
the number of neurons in the hidden layer of the MLP
model = Sequential([
Embedding(vocab_size, n_embd),
FlattenConsecutive(2), Linear(n_embd * 2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
FlattenConsecutive(2), Linear(n_hidden*2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
FlattenConsecutive(2), Linear(n_hidden*2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
Linear(n_hidden, vocab_size),
])
输入x的shape是32,8,27,其中32是batch_size,8是block_size,27是vocab_size。经过model的变化历程为:首先经过Embedding层,shape变为32,8,24,24是n_embedding,经过 FlattenConsecutive(2)变为32,4,24*2,经过 Linear(n_embd * 2, n_hidden, bias=False)变为32,4,n_hidden,然后Batchnorm和tanh层不改变shape,再次经过FlattenConsecutive(2)变为32,2,n_hidden*2,经过 Linear(n_hidden* 2, n_hidden, bias=False)变为32,2,n_hidden,然后Batchnorm和tanh层不改变shape,再次经过FlattenConsecutive(2)变为32,1,n_hidden*2,FlattenConsecutive会把32,1,n_hidden*2 squeeze 成32,n_hidden*2,经过 Linear(n_hidden* 2, n_hidden, bias=False)变为 32,n_hidden,然后Batchnorm和tanh层不改变shape,最后经过 Linear(n_hidden, vocab_size)变为 32,vocab_size
# parameter init
with torch.no_grad():
model.layers[-1].weight *= 0.1 # last
layer make less confident
parameters = model.parameters()
print(sum(p.nelement() for p in parameters)) # number of parameters in total
for p in parameters:
p.requires_grad = True
PS:如果Linear层不进行参数共享,而是单独定义context_length/2个linear层,那么应该重新定义custumlinear层,并且把FlattenConsecutive层集成 到custumlinear层中:
class CustumLinear:
def _init_(self,context_length,n, fan_in, fan_out): # n表示相邻n个字母进行组合 fan_in = C*self.n
self.n =n
self.context_length = context_length
assert context_length%n == 0 #保证context_length是n的倍数
#创建context_length//n个linear层
self.linear_list = []
for _ in range(context_length//n):
l = Linear(fan_in, fan_out, bias = True)
self.linear_list.append(l)
def __call__(self, x):
B, T, C = x.shape
x = x.view(B, T//self.n, C*self.n)
outputs = []
for i in range(context_length//n):
input = x[:, i , :] # input shape 是 B, C*n
//input = torch.reshape(input, ( -1,C*self.n)) # input的shape是(B , C*self.n)
output = self.linear_list[i]( input ) # output的 shape是 B, fan_out
outputs.append(output)
final_output = torch.stack(outputs, dim = 1) # final_output 的shape是 B,context_length//n , fan_out
return final_output
def parameters(self):
return